c p u ville logo
Donn Stewart
13917 Deviar Dr
Centreville, VA 20120
dstew@cpuville.com

Designing, Building, and Selling Obsolete Computers -- for Educational Purposes -- since 2004

c p u ville logo menu icon
8-bit processor kit home 8-bit processor kit Register display kit Z80 socket adapter kit 40-conductor connector Accessories Instructions News and issues How to order
Z80 Kits home Single-board computer kit Bus display kit for single-board computer Original computer kit Bus display kit for original computer Logic probe kit Serial interface kit Disk and memory expansion kit Accessories Instructions News and issues How to order
Projects home Z80 wire wrap Original processor 8-bit processor Standalone Z80 computer
Educational home Logic gates Decoders Registers Buffers AND-OR array logic
Z80 kits and projects Tiny BASIC CP/M Original processor 8-bit processor
Z80 kit videos 8-bit processor videos

ALU Design

photo of ALU board

The Arithmetic-Logic Unit (ALU) described here is part of my homebuilt computer processor (CPU). It performs the computer processor computations. These are the arithmetic operations (addition and subtraction) and the logical operations (AND, OR, XOR and NOT) that are done during execution of the corresponding machine instructions. The ALU also performs the program counter incrementation during the instruction fetch.

I built the ALU from simple logic circuits. I used AND, OR, XOR and NOT gates, and four-bit adders. Subtraction is performed by two's-complement addition, that is, by inverting and adding one to the subtraend.

The lower three bits of the instruction opcodes are used as ALU opcodes. A small AND-OR array provides the logic needed to interpret these opcodes. You may realize that the ALU will perform computations during the non-arithmetic instructions, like the jumps and memory loads. However, with these instructions, the control logic of the processor makes sure that the result is ignored (not written to the accumulator). Here is a diagram of the ALU design, for one bit. The carrys are rippled to the subsequent adders.

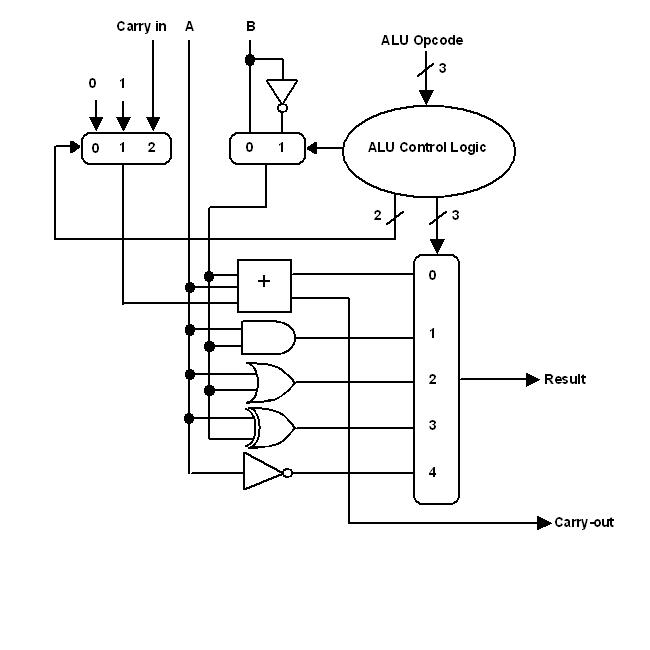
block diagram of ALU

The ALU performs the four logical operations and addition continually on every pair of operands. However, only the result selected by the output multiplexor (as determined by the ALU logic) will appear on the ALU output. The processor control logic determines if the carry result will be stored in the carry flip-flop on the main board.

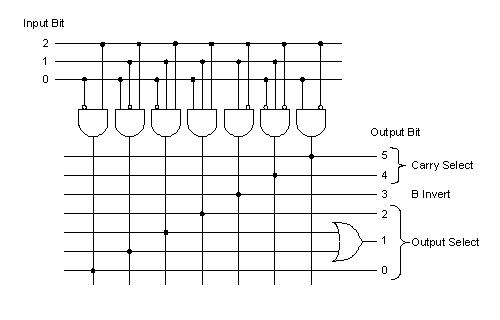
The ALU logic circuit is here. I used a one-of-eight decoder for the AND plane.

ALU logic diagram

There is a flaw in the ALU design, it does not perform subtract with borrow correctly. It will add the complemented carry (one bit), but to work properly it should add the two's complement of the carry. The two's complement of the carry would be a 12-bit value, and to perform properly the ALU would need an additional 12-bit adder to do this. However, one could still do subtract with borrow using software, by doing subtract, then subtracting one from the result if there was a borrow on the previous subtraction.

Links to Original CPU pages:

menu icon